اغلب اعداد حقیقی حتی برای ریاضیدانها ناشناخته هستند؛ اما چه عاملی این اعداد را متمایز میکند؟
عجیبترین عدد حقیقیای که میتوانید تصور کنید چیست؟ شاید بسیاری از افراد به اعدادی گنگ مثل پی یا عدد اویلر فکر کنند. در واقع این اعداد را میتوان «وحشی» توصیف کرد چرا که تا بینهایت رقم اعشار بدون ارقام تکراری ادامه پیدا میکنند؛ اما این اعداد عجیب همراه با اعداد گویا تنها بخش کوچکی از اعداد حقیقی را تشکیل میدهند که میتوانند در راستای یک محور حقیقی ظاهر شوند. این اعداد در واقع همان اعدادی هستند که در تمام انواع اندازهگیریهایی که میشناسیم مثل زمان، دما و فاصله کاربرد دارند.
به نوشتهی وبسایت ساینتیفیک امریکن، اگر بهصورت تصادفی عددی را روی محور حقیقی انتخاب کنید، با عددی محاسبهناپذیر روبهرو میشود. هیچ راهی برای محاسبهی دقیق این مقادیر وجود ندارد. اعداد حقیقی ترکیبی از اعداد گویا و گنگ هستند. اعداد گویا (اعدادی که بهصورت کسر p/q نوشته میشوند که در آن p و q اعداد صحیح هستند)، اعداد طبیعی (…، ۱،۲،۳) و اعداد صحیح (…، ۱،۲، . ، ۱-، ۲-،…) را دربرمیگیرند. بقیهی اعداد موجود در محور اعداد حقیقی، اعداد گنگ نامیده میشوند. این اعداد را هم میتوان به چند دسته تقسیم کرد که اغلب آنها فراتر از تصورات هستند.
بینهایتها، اعداد بسخرد، اعداد فرضی یا دیگر فضاهای عددی غیررایج بهسختی توصیفپذیر هستند. متأسفانه درک کامل اعداد حقیقی که فاصلههای جهان را توصیف میکنند کار سادهای نیست. برای درک این اعداد باید نگاهی به اعداد گنگ بیندازیم.
کدام اعداد گنگ هستند؟
تمام اعداد حقیقیای که نتوان با کسری از دو عدد صحیح نشان داد، گنگ هستند. از اعداد گنگ میتوان به ریشهی مربع ۲ اشاره کرد که دارای بینهایت رقم اعشاری بدون تکرار است. درواقع عدد رادیکال ۲ یکی از سادهترین اعداد گنگ ترسیمپذیر است؛ بهطوریکه میتوان با یک پرگار و خطکش و ترسیم مثلثی قائمالزاویه که دو ضلع آن دارای طول یک واحد هستند، به آن رسید. وتر مثلث هم دارای طول رادیکال دو است. بهطور مشابهی نسبت طلایی φ را میتوان بهصورت هندسی ساخت.
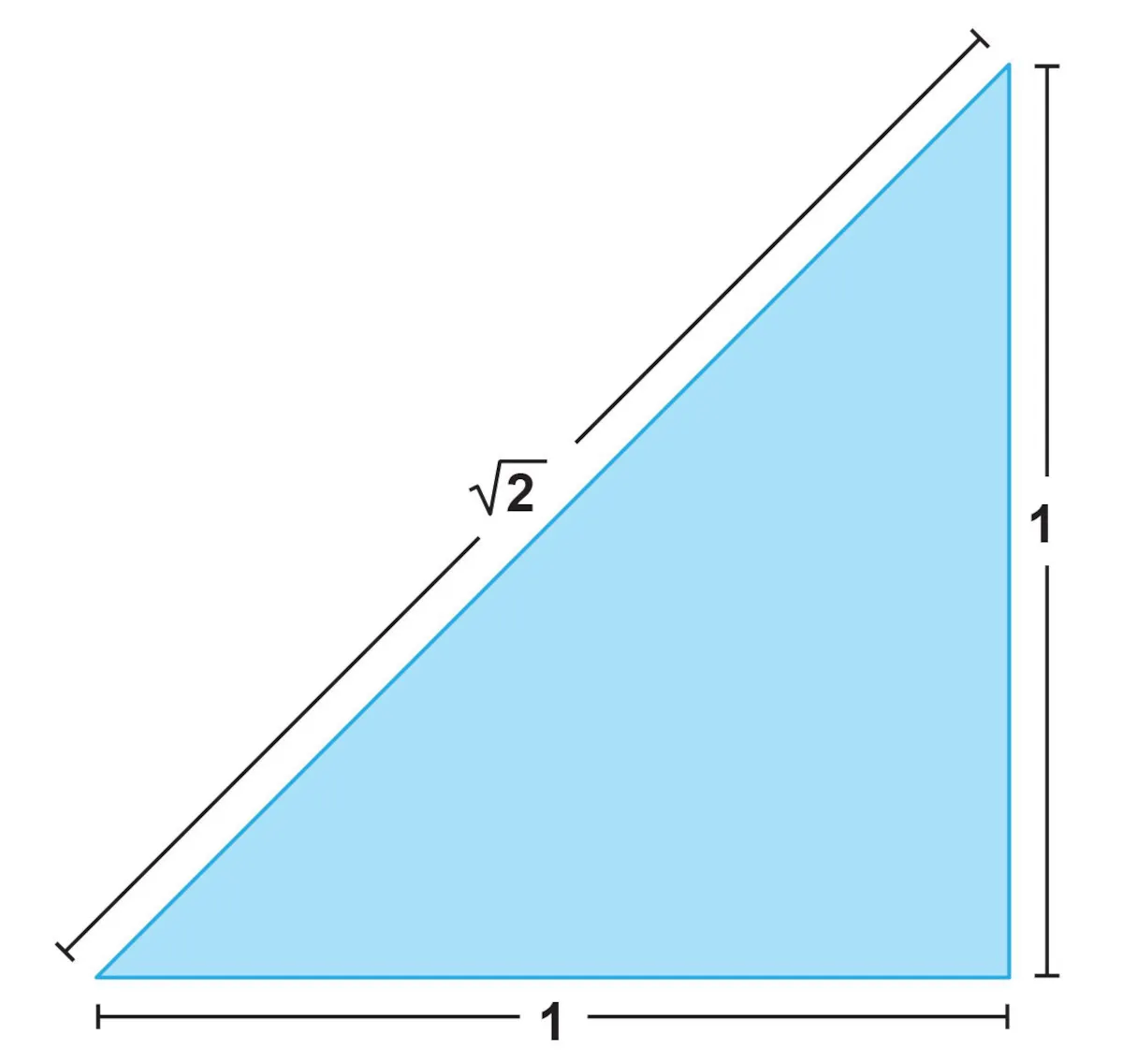
از لحاظ هندسی میتوان ریشهی مربع دو را با ساخت مثلثی قائم الزاویه با طول اضلاع «یک» ساخت. طول ضلع باقیمانده برابر است با ریشهی مربع ۲.
حتی در دوران باستان، افراد با اعدادی روبهرو میشدند که به شکل هندسی ترسیمپذیر نبودند. نمونهی بارز این عدد، دو برابر ساختن مکعب است. چگونه مکعبی با طول ضلع یک را میتوان به مکعبی با دو برابر حجم تبدیل کرد؟ بر اساس یافتههای پیر ونزل در سال ۱۸۳۷، طول یال ∛۲ لازم برای مکعب جدید را نمیتوان با خطکش و پرگار به دست آورد؛ اما ∛۲ در واقع متعلق به اعداد جبری است که میتوان به شکل راهحل معادلهی چندجملهای آن را به دست آورد. معادلهی متناظر برای ∛۲ برابر است با x^3 = 2.
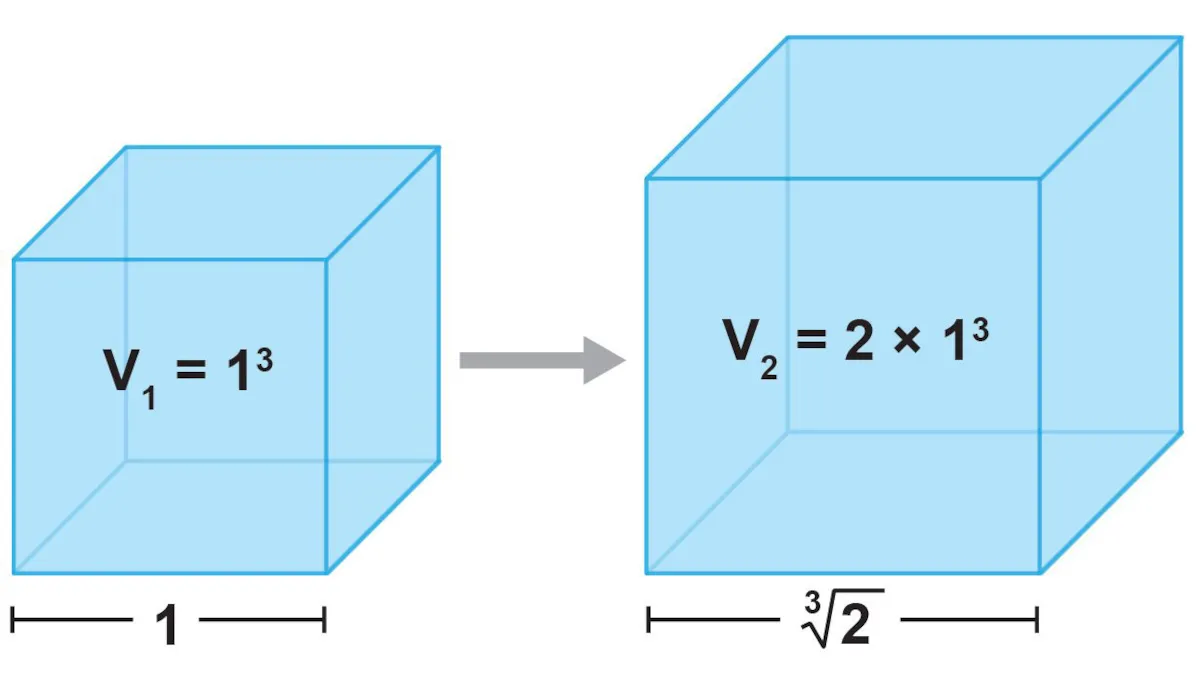
برخی اعداد گنگ را نمیتوان بهصورت هندسی ترسیم کرد. برای مثال، حجم مکعبی با طول ضلع یک را نمیتوان بدون استفاده از معادلهی چندجملهای ریشهی مکعب ۲ به دست آورد.
اعداد غیرجبری
اعداد غیرجبری هم وجود دارند که نمیتوان آنها را بهعنوان راهحلی برای معادلههای فوق توصیف کرد. هیچ فرمول سادهای برای محاسبهی آنها وجود ندارد. عدد π در این دسته قرار میگیرد؛ اما به این معنی نیست که مقدار آن را نمیدانیم. ارشمیدس، ریاضیدان یونانی به قانونی برای محاسبهی عدد π حداقل بهصورت تقریبی رسید. علاوه بر این الگوریتمهای متعددی وجود دارند که جایگاه اعشاری ۵۸۷ میلیونیم π را محاسبه میکنند. با در دست داشتن توان رایانشی و زمان کافی حداقل میتوان بهصورت تئوری این عدد را با دقتی مطلق محاسبه کرد. همین کار را میتوان برای عدد اویلر (e) یا ۲√۲ انجام داد.
اعداد غیرجبری رازهای زیادی را در خود دارند. با اینکه روشهای شفافی برای اثبات ترسیمپذیر بودن یک عدد وجود دارند، بهسختی میتوان ثابت کرد عددی «غیرجبری» است. برای مثال الکساندر گلفوند، ریاضیدان اهل شوروی در سال ۱۹۳۴ ثابت کرد عدد e^π غیرجبری است؛ اما اینکه مقادیر π^e یا π x e یا π – e جبری یا غیرجبری هستند امروزه هنوز مشخص نیست.
اعداد محاسبهناپذیر عجیب
تا قرن بیستم، افراد فرض میکردند اعداد غیرجبری، وحشیترین اعداد در زیرمجموعهی اعداد حقیقی هستند اما این فرضیه اشتباه بود. الن تورینگ، ریاضیدان بریتانیایی در سال ۱۹۳۷ مقالهای را دربارهی اعداد محاسبهپذیر منتشر کرد. او از این اصطلاح برای توصیف تمام مقادیری استفاده کرد که برایشان قانونی محاسباتی مثل الگوریتم وجود دارد بهطوریکه یک کامپیوتر میتواند مقدار عدد را با هر درجهای از دقت محاسبه کند.
تقریباً تمام اعداد غیرجبری شناختهشده مثل π و e در گروه اعداد محاسبهپذیر قرار میگیرند. در ضمن مقدار عددی تقریبی و روش محاسبهشان را میدانیم. تورینگ در پژوهش خود نشان داد اعداد محاسبهناپذیری هم وجود دارند که مقدارشان با دقت محض قابل محاسبه نیست. حتی بدتر از آن تقریباً تمام اعداد حقیقی محاسبهناپذیرند.
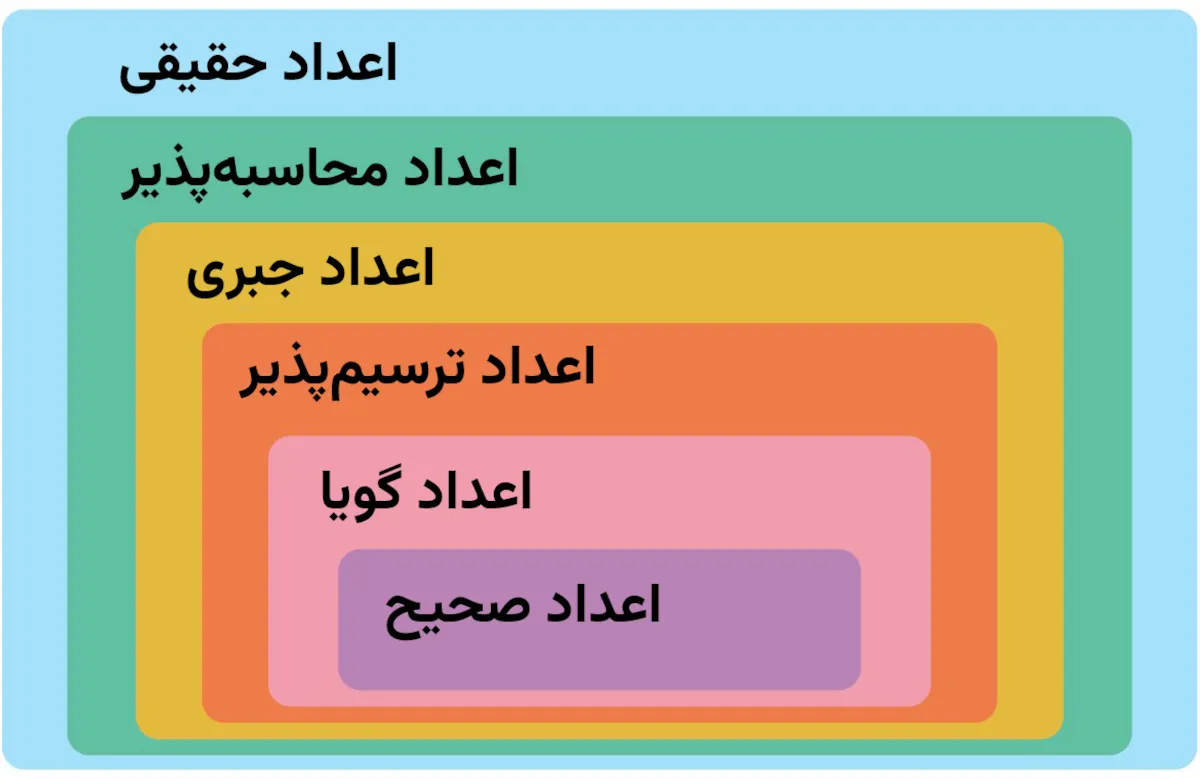
اعداد حقیقی دربردارندهی اعداد محاسبهپذیر، اعداد جبری، اعداد ترسیم، اعداد گویا و اعداد صحیح یا درست هستند.
با فکر کردن دربارهی اندازهی بینهایت مجموعههای عددی مختلف میتوان به حقیقت فوق پی برد. گئورگ کانتور ریاضیدان، بنیادهای این فرضیه را در اواخر قرن نوزدهم بنا نهاد. در آن زمان او نشان داد مجموعهای از اعداد طبیعی، صحیح و گویا دارای کاردینالیتی یکسان هستند (کاردینالیتی اصطلاحی ریاضی است که اندازهی یک مجموعه را توصیف میکند)؛ اما چگونه؟ برای درک این مسئله در ابتدا باید بگوییم قوانین محاسبهی اعداد متناهی را نمیتوان برای اعداد نامتناهی اعمال کرد. برای مثال اعداد طبیعی و اعداد صحیح را در نظر بگیرید: میتوان یک عدد مثبت و یک عدد منفی صحیح را به هر عدد طبیعی تخصیص داد و برای مثال به چنین مجموعهای رسید: (۰،۰)، (۱، ۱)، (۱، ۲)، (۲-،۳)، (۴،۲) و به همین ترتیب ادامه داد.
ازآنجاکه هیچ پایانی برای اعداد طبیعی وجود ندارد، میتوان به نگاشتی یکبهیک بین دو مجموعه رسید. این مسئله درست مانند تخصیص یک صندلی اتوبوس به اشخاصی است که در ایستگاه اتوبوس ایستادهاند. در این نمونه میدانیم بهاندازهی تعداد صندلیها، افرادی در ایستگاه اتوبوس وجود دارند. همین مسئله برای اعداد طبیعی و صحیح صدق میکند.
یک نگاشت یک به یک مشابه را میتوان بین اعداد طبیعی و گویا پیدا کرد. بر اساس محاسبات کانتور، کاردینالیتی اعداد طبیعی کوچکترین بینهایت ممکن است. او این مجموعه را «بینهایت شمارا» نامید.
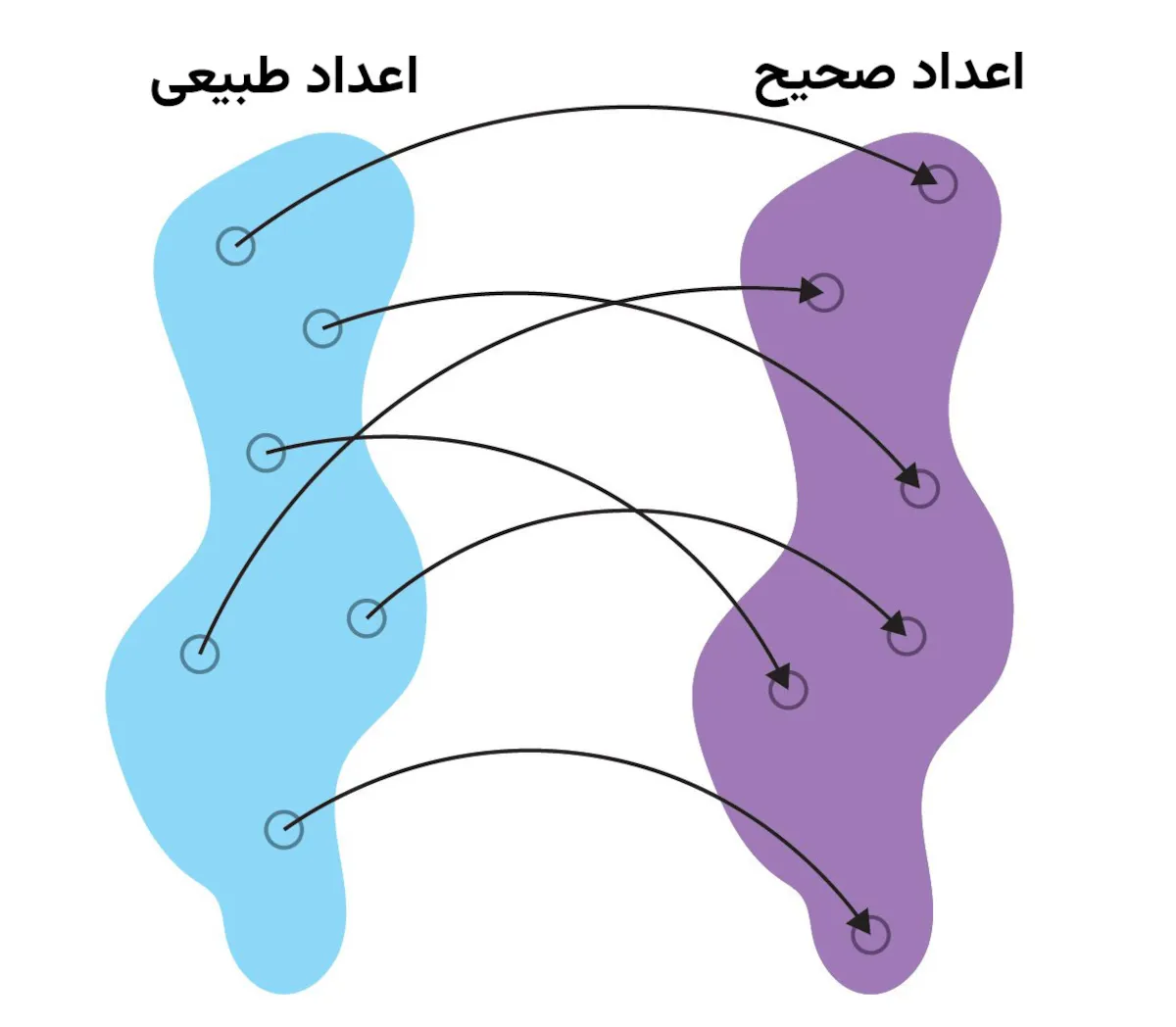
دو مجموعه برابر هستند، اگر نگاشتی یک به یک بین عناصر مجموعههای متناظر وجود داشته باشد.
از سوی دیگر، اعداد حقیقی را نمیتوان شمرد. کانتور ثابت کرد کاردینالیتی اعداد حقیقی لزوماً بزرگتر از اعداد طبیعی است. او نشان داد هیچ راهی برای شمردن تمام اعداد حقیقی موجود در یک فهرست بدون حذف برخی مقادیر وجود ندارد؛ بنابراین اعداد حقیقی نوعی مجموعهی ناشمارا هستند.
استدلال کانتور به این شرح است: فرض کنید شخصی فهرستی از تمام اعداد حقیقی را داشته باشد. میتوان این فهرست را به شکل یک جدول در نظر گرفت. در هر سطر عددی وجود دارد و هر ستون موقعیت جایگاه اعشاری را نشان میدهد. کانتور نشان داد اگر دایرهای را حول محور اعداد تشکیلدهندهی قطر مربع ترسیم کنید (برای مثال اولین رقم در اولین سطر، دومین رقم در دومین سطر و به همین ترتیب)، میتوانید با اضافه کردن عدد ۱ به هر ورودی قطر، عدد حقیقی جدیدی بسازید. این عدد جدید را دیگر نمیتوان در فهرست قرار داد؛ بنابراین فهرست اصلی شما از کل اعداد حقیقی ناقص خواهد شد.
اما استدلال تورینگ اینگونه بود که تمام اعداد محاسبهپذیر باید شمارا هم باشند. برای هر کدام از این اعداد میتوان ماشینی ساخت که مقدار آن را محاسبه کند. از آنجا که میتوان این ماشینهای محاسباتی را شمرد میتوان نتیجه گرفت که اعداد محاسبهپذیر لزوماً شمارا هم هستند. این نتیجه پیامدی برای اعداد محاسبهناپذیر دارد که بخش بیشتری از اعداد حقیقی را تشکیل میدهند: میتوان نتیجه گرفت که تعداد ناشمارایی از آنها وجود دارد.
بنابراین اگر احتمال روبهرو شدن با نوع مشخصی از عدد حقیقی را که بهصورت تصادفی ترسیم کردید محاسبه کنید، به نتیجهی واضحی میرسید: در صد درصد مواقع، این عدد محاسبهپذیر نیست؛ اما این به این معنی نیست که نمیتوانید عدد دیگری را ترسیم کنید. در مجموعهی نامتناهی از رویدادها، احتمال صفر به معنی غیرممکن بودن خروجی نیست. با توجه به این مسئله که تعداد زیادی از اعداد محاسبهناپذیر شناختهشده نیستند، فراوانی و تعداد زیاد آنها خود یک شگفتی به شمار میرود.
مسئلهی توقف بهعنوان منبع الهام
نمونههای اندکی از اعداد محاسبهناپذیر با مسئلهی معروف «توقف» در علوم کامپیوتر تعریف شدند. برای فرض این مسئله که توسط تورینگ توسعه یافت، کامپیوتری را در نظر بگیرید که مجموعهی مشخصی از دستورالعملها را برای حل یک مسئله اجرا میکند (به بیان دیگر کامپیوتر از یک الگوریتم استفاده میکند). در مسئلهی توقف از شما خواسته میشود ماشینی را فرض کنید که میتواند تشخیص دهد کامپیوتری که یک الگوریتم مشخص را اجرا میکند در نقطهای متوقف شود یا برای همیشه ادامه پیدا کند. بر اساس اثبات تورینگ، با اینکه ماشین میتواند تشخیص دهد که برخی الگوریتمها در یک زمان متناهی اجرا شوند، احتمالاً هیچ روشی وجود ندارد که بتواند این کار را برای تمام کدهای برنامه انجام دهد. مسئلهی توقف همان کاربرد مستقیم قضیههای «ناتمامیت» کورت گودل ریاضیدان است که نشان میدهد تمام عبارتهای ریاضی اثباتپذیر نیستند.
گرگوری چایتین، ریاضیدان آرژانتینی-آمریکایی از مسئلهی توقف برای تعریف یک عدد محاسبهناپذیر استفاده کرد. این عدد که ثابت چایتین Ω نامیده میشود، متناظر با این احتمال است که بر اساس آن مدل کامپیوتری (ماشین تورینگ) برای هر مقدار ورودی |Ω = –∑p½|p متوقف میشود که در آن p نماد تمام برنامههایی است که پس از یک اجرای متناهی متوقف میشوند و |p| طول برنامه را بر اساس واحد بیتی توصیف میکند.
بنابراین برای محاسبهی دقیق ثابت چایتین، باید بدانیم کدام برنامهها متوقف میشوند و کدامیک نمیشوند، که این کار بر اساس مسئلهی توقف، ممکن نیست. بااینحال، کریستین اس کلاود ریاضیدان و همکارانش، در محاسبهی اولین رقمهای ثابت چایتین عملکرد موفقی داشتند:
۰.۰۱۵۷۴۹۹۹۳۹۹۵۶۲۴۷۶۸۷….
بنابراین میتوان نتیجه گرفت که اگر برنامهای را بهصورت تصادفی به زبانی بسازید که کلاود و همکاران او از آن استفاده کردند، این برنامه با احتمال ۱٫۵۸ درصد در یک زمان اجرای متناهی حفظ میشود. حتی اگر نتیجه دقت بالایی داشته باشد، ثابت چایتین را نمیتوان با دقت محض محاسبه کرد.
عدد محاسبهناپذیر و سگ آبی مشغول
عدد محاسبهناپذیر دیگر از تابع «سگ آبی مشغول» (Busy Beaver) یا BB(n) به دست میآید. این تابع بزرگترین خروجی ممکن (بر اساس بیت) را که یک الگوریتم میتواند از n بیت تولید کند، محاسبه میکند.
برای مثال عدد محاسبهناپذیر از ساختار ذیل به دست میآید: ∑n½BB(n) . تاکنون تنها چهار رقم اول تابع سگ آبی مشغول شناخته شدهاند و دو رقم دیگر را میتوان تخمین زد.
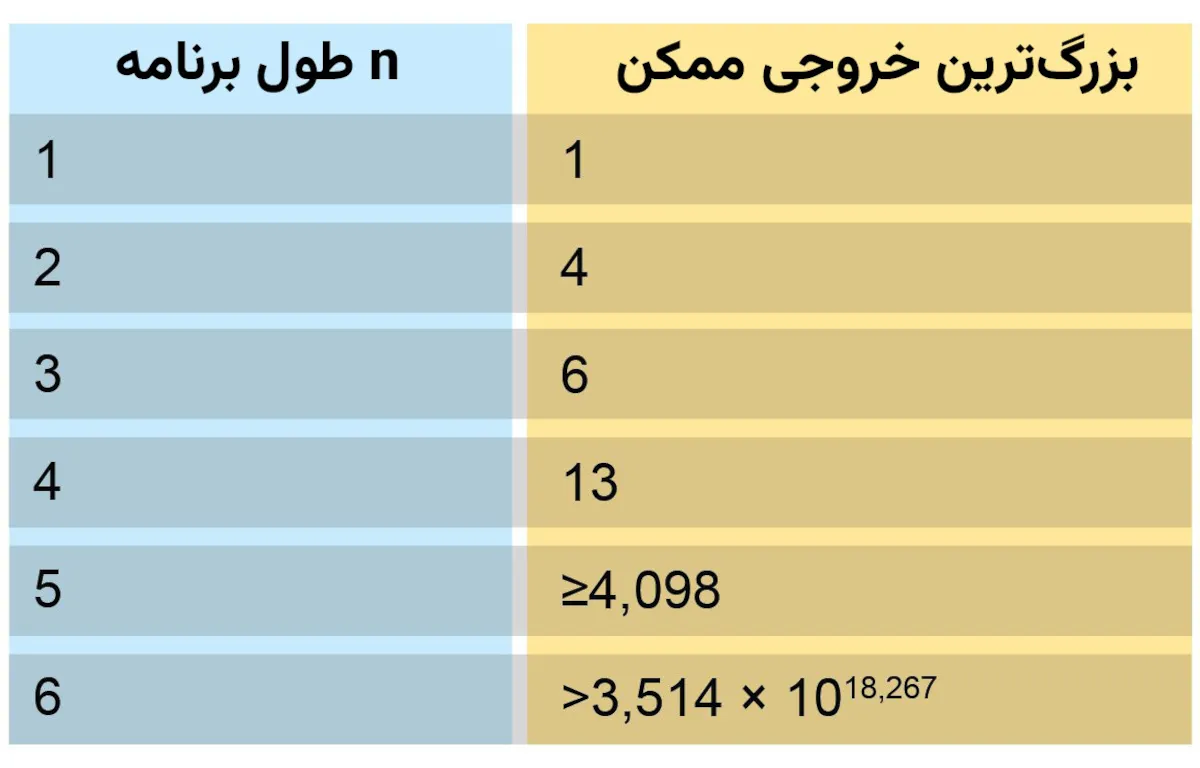
تابع سگ آبی مشغول، بزرگترین خروجی ممکن را که الگوریتم میتواند از یک تعداد مشخص (n) بیت تولید کند، محاسبه میکند.
بنابراین، اولین رقمهای این عدد محاسبهناپذیر با این فرمول به دست میآیند:
∑n½BB(n) = 0.51562548….
روشهای پیچیدهی دیگری هم برای تعریف اعداد محاسبهناپذیر وجود دارند. با این حال، با توجه به فراوانی اعداد محاسبهپذیری که میشناسیم، همیشه عجیب است که مقادیر محاسبهناپذیر در اعداد حقیقی و حتی در جهان غالب هستند.









